Black Holes and Transverse Tidal Effects,
a revised essay on some thoughts


This is a revised version of an essay from many years ago. I am still looking for help in the topic explored here. The content is meant to convey a set of insights that might be useful for further development. The earlier version appeared on December 25, 2016 and can be found at
Black Holes and Transverse Tidal Effects, a short essay on some thoughts

Abstract
It has been a common practice for the past many decades in the scientific field of gravitation concerning black holes, event horizons, and GR, to dismiss any effects of tidal accelerations by simply scaling the mass of the black hole up, thus reducing the local effects of gravity gradients to nothing. In this text, reasonable doubt is cast upon the practice of ignoring tidal effects and some of the results of not “sweeping tidal effects under the spacetime rug” are investigated.
Preface
The ideas presented here ought to seem like a completely obvious set, though you may need to be patient in order to slog through my reasoning. It has been a common practice in the world of black holes, event horizons, and GR to dismiss any effects of tidal accelerations by simply scaling the mass of the black hole up, thus reducing the local effects of gravity gradients to inconsequential magnitude. Indeed, the practice of ignoring tidal accelerations runs so deep that when I tried to ask a limited form of the central question presented here of UCB's Prof. Bousso at his colloquium in 2013, he dismissed the relevance of tides before I could even finish setting up the question.
The fact that I've tried to present this before, and had such poor luck in getting an understanding of the ideas across, is why I what follows is probably written in an overly detailed way. Please bear with me.
Tidal accelerations about gravitational central potentials, review
We start with the observation that the radial tidal acceleration causes a redshift of the spacetime ahead and behind an in falling observer, and the transverse tidal acceleration should cause a blueshift of the spacetime to the sides (transverse to the line of fall) of that observer. To understand why, consider a cloud of test particles all around a freefalling observer in a gravitating central potential (for example, the weak limit of the Schwarzschild potential).
Consider particles “in front and behind” along our test observer's radial line of freefall into a black hole, and consider test particles about our observer, transverse to his line of freefall. As our observer freefalls toward the hole, the test particles along his radial line of freefall will accelerate away from him because the gravitational field strength is changing as a function of radius from the center of the hole. Conversely, as our observer falls toward the central potential the test particles transverse to his line of freefall, those to his “left and right”, will be seen to be accelerating toward him. This is the transverse tidal acceleration and it happens because particles in freefall along different radial paths will have a component of their acceleration relative to each other that is parallel and a component that is perpendicular to their radial paths toward the central potential.
If we were to put the entire ensemble of observer and test particles inside a closed room (traditionally an elevator), that was likewise also in freefall, there would be no way for the observer to determine whether he was falling into the gravitational field of a compact object (a black hole), or whether he was in a universe that was expanding in one direction and contracting in directions perpendicular to that. The freefalling observer would only see that along one axis objects removed from him would accelerate away in proportion to their displacement, while along the other directions, they would accelerate towards him in proportion to their displacement. This setup is true in the limit of “small rooms” – and local acceleration effects. If the size of the room is not small in comparison to the distance to the compact source of gravity then there will be a few telltale signs our observer might use to suspect that he's in a gravity well instead of a strange universe with an anisotropic Hubble constant.
For small displacements along the radial direction from the gravitating body, the radial component of the tidal acceleration goes by
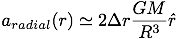
Where R is the radial distance from the gravitating body, and Δr is the separation of the test particles along the radial distance. However, when the separation, Δr , along the radial is not small in comparison to the radial distance, R , then one should use the difference between the local accelerations
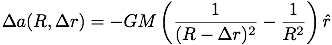
which clearly grows faster in magnitude for displacements towards the gravitating mass than for equal displacements away from it. So, for an extensive enough observer and test particle ensemble (all enclosed in a big enough “room”), the observer might suspect that he's near a compact source of gravity (with the inverse square law in play), rather than in a universe with a strange Hubble constant. However, the Equivalence Principle would not allow our observer to conclusively know which one is the “true” external situation without actually looking outside the room. All of the signals sent from or between test particles in his freefalling “room” would behave just as if there were an anisotropic Hubble constant at work.
For small displacements the magnitude of the transverse tidal acceleration is 1/2 the magnitude of the radial tidal acceleration, in the direction transverse to the radial from the gravitating source:
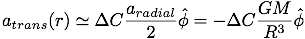
Where ΔC is a distance along the circumference of a circle of radius R (and transverse to the radial direction). The transverse tidal acceleration scales by the inverse radius from the point of gravitational attraction. And it also scales by the inverse square distance from the gravitating source to the freefalling observer. Thus, the total scaling is by the inverse cube of the radius – over a given distance transverse to the radial acceleration. However, as with the case for the radial tidal acceleration, that is only true for small displacements. Over larger displacements, where ΔC is not small compared to R , the above approximation fails because, while the radial tidal acceleration is due to the gradient of the (inverse square) acceleration law, the transverse tidal acceleration is actually due to the angular separation of the radial paths of the infalling test particles.
The equation for the transverse component of the tidal force is something like
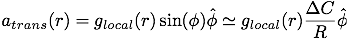
Where glocal(r) = -GM/r2 and φ is the angle (in spherical coord.) separating the freefall radials of the test particles (with the coord. center at the center of the black hole). The approximation of the transverse tidal acceleration for small displacements comes from the fact that the sine of a small angle is approximately equal to the transverse displacement divided by the axial displacement (φ ≃ ΔC/R).
I contend that the correct way to look at the transverse tidal acceleration is that it is the component of the local acceleration felt between two freefalling test particles, falling along different radials, that is, not parallel to each other. Thus, I think, a "cleaner" way of thinking about the transverse tidal acceleration is that it scales with angle (φ) around the gravitating body, not by linear distance between test particles, concluding our review of tidal accelerations.
Effects of tidal accelerations on horizon radiation
Hawking radiation, as seen from far away from the source, is emitted from just above the black hole event horizon. The radiation starts out as Planck-scale photons (E ∼108 J) but is strongly redshifted on its way to observers far from the hole. Hawking radiation from a 1 Solar mass black hole is at a temperature of T ∼ 10-7 K , as seen from afar. The redshift comes from the fact that the "surface" emitting the radiation is itself in radial free fall with a speed of just about c , away from observers distant from the hole.
If we take on the point of view of an observer freefalling into the hole, then the event horizon will seem to "fall away" from our observer as he approaches the Schwarzschild radius (where the event horizon is seen to be by observers far from the hole). The best description I know of why this is so is this:
Imagine an observer falling into the black hole accompanied by a series of test particles in front and behind him. For simplicity we'll consider that the infalling observer has no angular momentum with respect to the hole and so falls along a simple radial path (with respect to the hole). The test particles are arranged to fall along the same radial path.
As our observer falls he notices no local gravity, but he does notice that the test particles in front and behind him are accelerating away from him. The ones farther away have a larger acceleration. This is the radial component of the tidal force.
Now, if the test particles are emitting radiation at a known energy it will be more and more redshifted (as seen by him) as the particles accelerate away from him to higher and higher relative recessional speed. Here's the key to why Hawking radiation is seen to still be very low energy, even for an in falling observer: the radiation is always seen to be coming from a “surface” (an event horizon) which is in free fall away from the observer. Thus the radiation is always seen to be redshifted to a very low energy.
The situation is caused by the Equivalence Principle: the event horizon itself can not be a special place that an observer can detect traveling through. If we imagine a black hole massive enough then we can neglect tidal forces because the gravity at the Schwarzschild event horizon can be made arbitrarily small while the radius of the hole is made arbitrarily large. Thus, the reasoning is that there can't be anything special about the event horizon at the Schwarzschild radius. Or so the “usual story” goes.
As noted above, the problem with the "usual story" is that it does not treat the measurement of tidal forces the same way as other black hole features. Tidal forces are usually dismissed on the basis that over a given length, the force can be made to go to as low a value as we want by proposing a massive enough black hole, with a slowly enough changing local gravity field. However, most of the other important features of black holes are described in terms of multiples of the Schwarzschild radius (or rS, because I'm getting tired of typing that), so that they are mass scale insensitive. It is this mixture of mental models that I believe has caused the ideas here to be overlooked or misunderstood.
What I think I have found is that by treating tidal forces as acting over a scaled distance – radial distances measured in multiples of rS and circumferential distances measured as the angle around the hole's center – we come to a very different picture of what happens to an infalling observer than the current paradigm would have us conclude.
An absence of transverse tidal effects in Hawking's original paper
Since this is a revised version of the essay I have had a bit more time to think and read about the ideas presented. Having now read I have a few additional observations.
In the 1975 paper by Stephen Hawking titled _Particle Creation by Black Holes_[1] there is an absence of consideration of the tidal effects, transverse or otherwise. There are several places in the paper where approximations were made such that only radial (and time) factors would be included in the calculations that he produced.
The approximations I saw were:
-
1.The use of Penrose diagrams, which exclude any effects that might arise from paths around the hole because they include only radial and time coordinates.
-
2.The use of restricted, local patches of spacetime "of radius ~M", which will again exclude tidal effects by their construction as locally flat portions of spacetime.
These approximations would effectively exclude what I'm trying to point to in this essay from consideration in Hawking's original work showing black hole radiation.
Section 4 of the paper, "The Back-Reaction on the Metric", contains a description of an observer falling through the event horizon. This looked promising until I noted that the analysis was carried out in a local patch of the spacetime "of radius ~M" at the horizon (see #2 above). The analysis contained some consideration of Hawking radiation modes with angular momentum encountering a centrifugal barrier, but it was only concerned with the modes that had low enough angular momentum to escape to infinity not with (trapped) modes behaving as pointed to by this essay.
More recently it has been pointed out to me that the wave equation used in Hawking's 1975 paper must have been
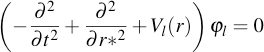
and that the potential term must have been

But the given wave equation here has no derivatives in directions other than r and t – but nothing in the angular directions. Therefore it can not include momentum transport in the spatial directions transverse to the radial direction. This makes sense for an analysis of radiation effects from black holes as seen from far away (in the “far field”), but can not be a complete description of what may be happening close to the hole (in the “near field”).
However, the gist of the question posed in my essay is the interaction between a radially infalling traveling wave (or particle, or observer) and a trapped wave/particle in the thermal atmosphere near the event horizon. I am specifically not puzzling here about the waves that escape to infinity that are the Hawking radiation itself.
Further, I would have thought that if there was a contribution to black hole radiation from the effect I'm proposing then there ought to be a difference between Hawking radiation and Unruh radiation. But there is no difference in their forms. So either the contribution from the effect proposed here is identically zero, or it was left out of the calculation. Based on the use of Penrose diagrams and/or restricted (locally flat) patches of spacetime in Hawking's original analysis, I'm guessing its the later.
The idea
While it may seem reasonable to propose that tidal accelerations near event horizons can always be “scaled away” by conducting our thought experiments in the vicinity of very massive black holes, the proposal is in fact a deceptive error. While local tidal acceleration (say, at r S ) can be made small by increasing the mass of the black hole by an arbitrarily large amount, increasing the mass of the black hole also increases the path lengths over which the tidal effects are integrated:

Test particles under transverse tidal acceleration along some circumferential displacement will have a kinetic energy increase proportional to their mass, times the tidal acceleration, times the displacement. (Clarification: kinetic energy relative to other freefalling test particles would increase because we are considering accelerations relative to other test particles.) Thus, in the case of the transverse tidal acceleration near black hole event horizons, one can not simply “scale away” the effects of tides by resorting to arbitrarily massive holes because the characteristic distances over which the accelerations take place themselves scale proportional to the mass of the hole, which cancels the scaling of the accelerations inversely to the mass of the hole. The energy effects of tidal accelerations (integrated over distance) are thus insensitive to changes in the mass of the black hole and can not be “scaled away”. All of which leads to some interesting consequences.
A thought experiment
In order to escape to infinity, photons of Hawking radiation must have very, very little orbital angular momentum about the black hole (it must be very closely “s-wave”). If a photon has “too much” orbital angular momentum it means that the radial component of its total momentum will be insufficient for it to escape. This is so because a photon's momentum and velocity vectors are aligned and if there is too much of its total velocity tangent to the horizon then it will have too little radial velocity to escape. As noted below, the upper limit to an escaping photon's orbital angular momentum is about 4 or 5 times Planck's constant.
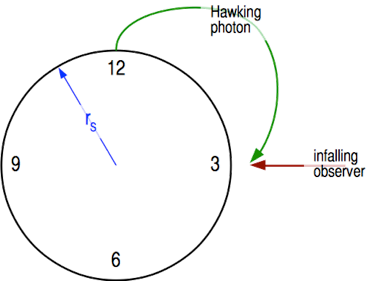
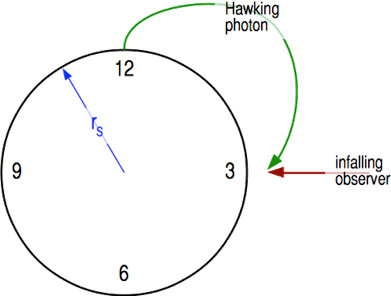
Figure 1: Observer intercepting a trapped Hawking photon.
Somewhere along his path into the black hole our observer will encounter the photon of trapped Hawking radiation. From his perspective the photon has been accelerating towards him, due to the transverse component of the tidal acceleration, all along its path from its emission near the horizon. In other words, both the photon and the observer have been accelerating towards the center of the black hole and have a component of their acceleration that “points at each other” for the whole duration of the thought experiment.
Figure 1 shows a diagram of the black hole set up so that rS is the face of a clock, with “12 o'clock” at the diagram's top, and the observer outside the hole's horizon and falling towards it along the “3 o'clock” radial path. Imagine that the test particle of Hawking radiation that is on an intercept path from the horizon to observer was emitted from “12 o'clock” and is following a (curved looking) geodesic from “noon” to intercept the observer near the “3 o'clock” position just outside rS.
From the perspective of the free falling observer, the Hawking photon will be blueshifted by the transverse tidal acceleration along its intercept path because both are accelerating along converging radial paths. The total integral of acceleration over the photon's path will (I think?) be something like the General Relativistic form of
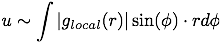
(With the caveat that the photon is actually following a geodesic – a straight line in its freefalling frame – which may lead to something very different from the equation above! Hence, my need for help with this stuff.)
Additionally, the integral of acceleration over distance gives the Hawking photon an exponential blueshift just like the redshift of a photon leaving the vicinity of the event horizon is exponential. As the particle is accelerated it picks up energy (from dE = F⋅ds = ma⋅ds ), but since energy has mass, the increment of energy the particle picks up over a distance ds1 also picks up more energy during the next distance interval, ds2. And so on, as exponential growth.
If the Hawking photon follows a sufficiently long path (in terms of angle φ) to intercept the freefalling observer from whatever patch of horizon emitted it, then it will have been accelerated through a total potential comparable in magnitude to the potential from flat space to the region of space at the horizon which emitted it. Let us compare the radial Newtonian potential from rS to infinity with the transverse tidal Newtonian potential.
The Newtonian potential from rS to infinity isUr = 2GM/rS where rS = 2GM/c2 so that Ur = c2, which is the total rest energy of matter transported from rS to flat space. The maximum possible (but see below) "Newtonian" potential for a transverse tidal blueshift from all the way around the backside of the hole's horizon is (something like) Ut = πGM/rS = c2π/2, which is larger than the total potential of the matter's rest mass.
However, the crude approximation above does not include the fact that in the curved spacetime near rS , the total angle around the hole, and projected onto the spacetime, is probably less than 2π because of its “funnel-like” structure seen in embedding diagrams of the Schwarzschild metric. Also, due to the exponential nature of the relativistic accelerations (where accelerated mass takes on more mass to accelerate), the Newtonian potential is not the correct thing to use, but the comparison does give an indication that the transverse tidal acceleration could in fact be as significant a blueshift as the event horizon's redshift. The two Newtonian potentials are of similar magnitude, so the relativistic potentials are likely significantly similar (though one is a redshift while the other is a blueshift). Again, I need help with this.
As noted above, due to the scale invariant nature of the product of transverse acceleration and path length, the blueshift factor is the same for any path starting at φ1 and ending at φ2 about a black hole because the acceleration scales inversely with the hole's mass while the length of the path from φ1 to φ2 scales with the mass of the hole (for paths at a given radius relative to the Schwarzschild radius (r/rS)). In other words the proposed blueshift effect seems to be insensitive to the black hole's mass.
In our example, continued from above, as the observer approaches the horizon in freefall he sees a ring of blueshifted Hawking radiation that has been emitted from around the edge of the event horizon (from “over the horizon” of the event horizon). The farther around the black hole the radiation comes from, the more it will have been blueshifted, with maximal blueshift for photons that travel 180 degrees around the black hole. As I mentioned above, the shift would be exponential with angular distance around the hole, and the trapped radiation would be blueshifted by a constant scaling factor for any mass of black hole. This would lead to a multiplication of the Hawking temperature, as seen by a freefalling observer passing close to the event horizon, by some gigantic, but universal factor.
But where is all the energy coming from to amplify the Hawking radiation? It would have to be coming from the energy of the hole itself. As the observer freefalls towards the horizon he is baked by a ring of blueshifted Hawking radiation and the energy in that radiation is the hole evaporating as he falls into it. The (blueshifted) hawking radiation goes to higher and higher temperature as the hole evaporates “under his feet” – and the observer never reaches the horizon or the hole.
And the best part is; The mechanism that demands this blueshifted "ring of fire" is none other than the Equivalence Principle itself because an acceleration, tidal or not, is the same as gravity. This looks a lot like a good solution to the Firewall paradox, because instead of violating the Equivalence Principle, this version of a Firewall is demanded by it.
Pathway to a solution
What this essay is in search of is a “simple” ray tracing exercise that follows in the footsteps of the thought experiment above. The setup would be a Schwarzschild (non-rotating, not charged) black hole spacetime and the “ray tracing” task would be to follow a photon that was emitted from very near rS and which follows a path through the curved spacetime to intercept an infalling observer. Would the photon be significantly frequency shifted? I suppose it would depend at least on the radial location of the observer because of the radial redshift that would be imposed on the photon climbing out of the hole's potential well, and then falling back to the observer. However, if the observer is positioned at the same radial distance from the center of the black hole as the point at which the photon is emitted then there ought to be no redshift from the black hole's potential well. However, this essay would argue that there will be a blueshift of the photon (as seen by the intercepting observer) if the emission and absorption locations have an angular separation about the hole, even if emission and interception happen at the same distance from the hole's center.
Some additional thoughts
-
Caution:Can we still use spherical coordinates in the spacetime near the event horizon? Its clear that they work somewhat near the hole, but is this a valid way to think about the dynamics near the horizon?
-
Caution:The embedding diagram for a Schwarzschild black hole is somewhat funnel-like near the event horizon. As noted already, that “funnel-like” structure would decrease the total projected angle φ on the spacetime embedding sheet. The total angle around the event horizon is 2π (a circle on the sheet) but the integral of the angles between radial "normals" of the horizon would be less than 2π because on the sheet they are tilted and lie on the surface of the "conic" portion of the embedding sheet. (However, I don't think the total angle is zero because the embedding sheet is not a parallel-walled "tube" at the event horizon like the way the gravitational potential diagram is.)
-
Caution:It my well be that the perceived transverse tidal acceleration near the event horizon goes to zero because of spacetime curvature issues. This would be the case if a) an observer falling to the event horizon sees the horizon as a flat surface because of the curvature of light rays, and b) gravity follows light paths. Or is this redundant with my caution about the embedding surface – just two ways of looking at the same effect? In which case the horizon does not go all the way flat for an observer falling through it or else the embedding surface would necessarily have parallel sides – which it doesn't at the horizon.
-
Caution:What is the population of strongly blueshifted Hawking photons? Even if there is a blueshift due to transverse tidal accelerations it still may not count for much if the total energy in the blueshifted radiation is small. Turns out that there may be an answer to this (see below), and that the numbers could be huge, with remarkable implications.
Implications?
Here is a short list of some possible, non-trivial items of theory and observation that will follow from an affirmative answer to the blueshift question I pose in this text.
-
1.The existence of something very much like a black hole firewall (that would in fact be demanded by the Equivalence Principle).
-
2.The resolution of the paradox of stationary vs. infalling observers w.r.t. Hawking radiation and black hole evaporation.
-
3.Modification to the spacetime metric close to black hole event horizons to account for the energy bound up in the "thermal atmosphere" of (trapped) Hawking radiation with high angular momentum.
-
4.Existence of a high viscosity, high density photon field in the near vicinity of black hole event horizons.
-
5.Small modification of the expected gravity wave spectrum from matter falling into black holes – small modification to last instant of "ring down". This one is experimentally testable!
-
6.Experimental test of Hawking radiation via the detection of gravity wave spectra conforming to the new modified metric and high viscosity "atmosphere" near black holes.
-
7.Experimental test of whether black holes are "black" vs "very dark brown" – which is slang for whether black holes form in finite time vs the classical, asymptotic infinitely slow collapse.
-
8.I'm sure there is more that I haven't thought of yet, so let me say "etc."
If the blueshift actually exists the way I think I'm proposing here, then there is a super intense field of trapped Hawking radiation near the surface of black holes. Objects falling through this radiation field would be subjected to optical forces, like the way optical tweezers work (see https://en.wikipedia.org/wiki/Optical_tweezers), and would be very strongly damped in their motions because the object's orbital motion (relative to the hole) would cause trapped Hawking radiation coming from the direction of the object's angular motion to be blueshifted a little more than radiation coming from behind its angular motion. A small blueshift of a very large number of photons could be a very large force if there are an extremely large number of trapped photons. So, the question is, how many photons would their be in the trapped "optical atmosphere" about a black hole?
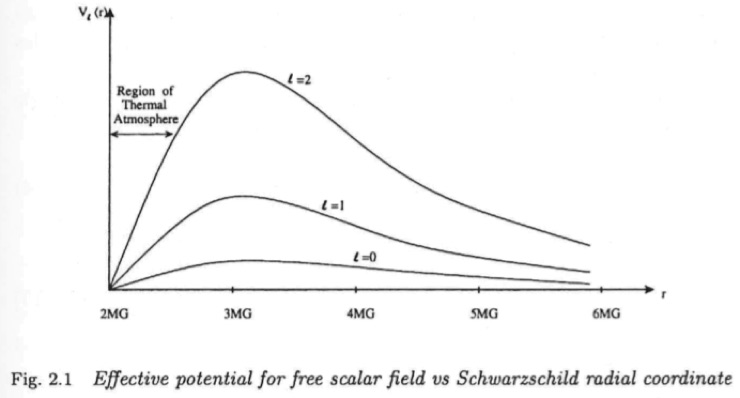
Figure 2: Figure 2.1 from page 27 of Leonard Susskind's Black Holes, Information and the String Theory Revolution showing the effects of the centrifugal barrier potential on escaping Hawking photons. Note the term “Region of Thermal Atmosphere”.
On page 27 of Leonard Susskind's _Black Holes, Information and the String Theory Revolution_[2] (see attached excepts at end) there is a figure showing the "effective [centrifugal] potential (Figure 2 here) for free scalar field vs Schwarzschild potential". From the figure it is clear that the only Hawking photons that can escape the hole's potential – at all – are those with extremely low angular momentum. Low being less than about 3 or 4 units of orbital angular momentum. For what I just typed here to have any meaning I need to provide some context.
The initial wavenumber of a Hawking photon at the Schwarzschild radius is about 1035 /m (an escaping Hawking photon gets redshifted from near the Planck energy to an energy corresponding to wavenumber of ∼1/rS when climbing out of the hole's radial potential, as seen by distant observers). If the Schwarzschild radius is, say, 2 km in radius (for a ~1 Solar mass black hole) then the angular momentum of a Hawking photon traveling tangent to the surface of the stretched horizon could be as high as
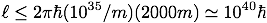
Now, if only the photons that are nearly S-wave (0 ≤ ℓ ≤ 5) have any chance to escape, and the allowed orbital angular momentum can go as high as 1040, then there can be a really huge number of photons trapped near the hole. (The reason why the photons with ℓ > 5 can't escape is that their wave vector is not close enough to exactly normal to the hole's surface.) And by "really huge" I mean that given all possible angular momentum states from 0 to 1040 in the "u" direction about the hole, times an equal number of states in the perpendicular "v" direction, we have a total available state space for the photon angular momentum of about 1080.
Actually this 1080 is an incorrect estimate that I made for an earlier draft of this essay. It represents only the available trapped photon states originating at a single patch of the horizon. The more correct number would be found by integrating over the whole surface similar to how the number of phonon states are found in the Debye model but taking the Debye temperature as the Planck temperature. I think. Anyway, the point is that it is a really huge number of trapped photon states in the vicinity of the hole's horizon and the real calculation is unimportant for the purpose of this essay.
Of those 1080 states, all but ~10 are states of trapped Hawking photons comprising the “thermal atmosphere” noted on page 27 of Susskind's book. That is why the emission rate of Hawking radiation, as seen from far away from the hole, is so small – most of the available photon states have too little of their momentum normal to the event horizon to escape.
However, if there are 1080 states available for trapped Hawking radiation, then there are likely to be a really huge number of photons in the trapped "atmosphere". Even if the energy of the individual photons is small there can still be a super intense optical field that infalling matter would encounter, near the Schwarzschild radius, on its way into the black hole. For example, even if we treat the photons as having only the energy they'd have after climbing out of the hole's potential (in other words as ordinary Hawking radiation at T ∼ 10-7 K seen from afar), then the total energy in the optical atmosphere could still be huge:
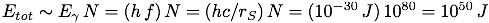
Where Eγ is the energy of a single (escaped, low angular momentum) Hawking photon as seen from far away from the hole, rS is the Schwarzschild radius, and N is the approximate number of photon states available. Putting this in terms of the black hole's mass we get
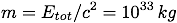
Which, for a ~1 solar mass black hole, is about as much mass as the hole itself! And, since the number of available trapped photon states, N, scales with the surface area of the event horizon, and the photon energy of each mode, as seen from far from the hole, scales as the inverse of the hole's radius, we have yet another scale invariant quantity. The trapped photon atmosphere is of the same relative mass magnitude independent of the black hole's mass.
Clearly there is a balance struck where the mass of the hole isn't outside the hole, or there would be no event horizon to generate the blueshifted trapped Hawking radiation, but I think you might be getting an idea for the energy scale in spite of the gross approximations I've made. Now, with that said, here are a couple of testable consequences. If there is a substantial portion of the hole's mass trapped outside the horizon, in the form of a trapped particle atmosphere, then:
-
•There ought to be a modification to the spacetime metric near the exterior of the hole's horizon. This modification of the metric ought to be observable as a change in orbit shape and decay rate, due to a departure from a Schwarzschild solution, during the very end stage of black hole collision/coalescence by gravity wave detectors.
-
•There ought to be some modification of the gravity wave emission that would correspond to the huge drag effects of the trapped atmosphere during the very end stage of black hole collision/coalescence by gravity wave detectors.
Here I might suggest that a better set of calculations be made to show that the trapped radiation is a prediction of extending Hawking's idea to include the interaction between the trapped radiation and the transverse tidal blueshift. If the existence of the trapped radiation is shown to be an unavoidable consequence of Hawking's theory, then there is a method of testing the theory. And from there it doesn't matter whether experimental evidence shows the existence of the trapped radiation or not because progress will thereby result from showing the existence or non-existence of Hawking radiation. Also, if Hawking radiation exists, then there is a need for a Black Hole Firewall, but if Hawking radiation does not exist, then there is no need for a Firewall. Thus, the proposed solution for the Firewall Paradox proposed here is nicely matched to whether it is actually needed or not.
And that's about all I think I know about that. It has been about 20 years since I was any good at manipulating the mathematics required for solving problems in General Relativity. Any help with that would be most appreciated.
References
[1] S. W. Hawking. Particle creation by black holes. Comm. Math. Phys., 43(3):199–220, 1975.
[2] Leonard Susskind. An introduction to black holes, information and the string theory revolution (river edge, 2005.
Monday, July 13, 2020
by David Woolsey