 |
| figure 1: Etalon transmission vs. length for l = 6328Å and R = 0.9 |
v. 1.1, (2000.04.11)
David Woolsey
The simple description of this device is it is just another optical cavity that can be brought in and out of resonance by changing its length. It consists of a confocal resonator cavity of 2.5 cm in length (called an etalon) with a piezoelectric actuator to sweep its length over a narrow, but significant, range. As the length of the cavity changes so does its resonant length criteria and thus its tranmissive properties as a function of frequiency. On one side of the cavity is the laser and on the other side is a photodetector which responds to the light intensity passing through the etalon. The resulting disply on the oscilloscope is a spectrogram of the laser output mode structure with intensity plotted as a function of frequiency (figure 1).
|
The sharpness of the peaks in the spectrogram is limited by the finess of the etalon. The finesse is the ratio of the etalon's Free Spectral Range (FSR) to the width of the peaks at half maximum. The FSR is the interval between adjacent transmission peaks of the etalon and is equivalent to the cavity mode spacing of the laser in that it comes from the same kind of resonance criteria. The FSR of this interferometer is 3.0 GHz as found from the Dn = c/RT formula in the lab instructions.
Dn = c/RT = c/4·L = (3·108 m/s)/(4·2.5 cm) = 3.0 GHz
For me the measured width of the peaks was [NEED MEASUREMENT] which leads to a finesse of F* = width/FSR = [NEED RESULT]
From the known finesse we can determine what the mirror reflectivity is as follows:
F* = p·(R)1/2/(1-R) --> R2 - ((p/F*)2+2)·R + 1 = 0
Solving for R we get
R = 1 + 1/2(p/F*)2 ± 1/2(p/F*)·((p/F*)2+4)1/2
|
The factor of four in the round trip length (RT) in the calculation of FSR comes from the fact that the light in the confocal etalon cavity travels in a kind of "angular figure eight" rather than straight back and forth between the mirrors (figure 2). The distance between the mirrors is twice the focal length which is the same as the radius of curvature. Thus RT = 4·L = 4·(2.5 cm) = 10 cm.
If we had been using a flat-flat etalon the round trip distance would have been calculated, just like the laser cavity, as 2·L. The reason for not using a flat mirrored etalon is that it would be very much more sensitive to angular misalignment. The confocal type is almost a cylindrical "core" out of a spherical mirror in construction and so is essentially impervious to angular misalignment and only a little more sensitive to lateral misalignment.
This measurement used to be made with a Michaelson type interferometer but has been changed to the more direct method of using a Fabry-Perot type interferometer. The use of a confocal Fabry-Perot interferometer allows a more direct and fool-proof means of making this measurement when set up as follows (figure 3).
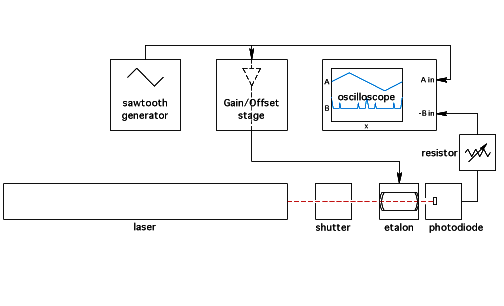 |
| figure 3: Setup of Fabry-Perot interferometer |
On and warmed up for about 20 minutes. While it's warming up you should take time and care to level it to the midpoint height of the beam steering mirrors. Leveling is not necessarily needed but you may thank yourself later for doing it.
Open and with beam passing through it.
Set for 100 Hz sawtooth output at about the midpoint of the output gain. A ramp in the appropriate direction is what we really want but a sawtooth is what we have (a good way to get a ramp is to take it from the horizontal sweep of the oscilloscope, but this modification has not been done to the 'scope). A sweep frequency that is too low will be annoying to look at while one that is too high risks driving the interferometer into a non-linear operation. Likewise an output amplitude that is too high will cause it to operate in a non-linear region (one that is very asymmetrical as well).
What you want to see are two complete sets of peaks on each side of the ramp. You need two sets because the distance between them is the (known) mode spacing, or FSR, of the etalon cavity while the distance between peaks within a set is the (unknown) mode spacing of the laser cavity. Adjust the amplitude of the sawtooth so that you have the required number of peaks.
Turn this on with the knob set to its midpoint. Adjustments to the offset control will shift the positions of the peaks right or left on the 'scope display. This adjustment should not really be needed for our use because the peaks will slowly drift on their own.
Align the etalon so that the beam passes through it on axis and such that the reflection from its surfaces is not going back into the laser output mirror. If the light is scattering back into the laser cavity it will cause mode hopping, output power fluctuations, and in extreme cases cause the laser to cease lasing intermittently. Note also that the signal through the etalon is somewhat sensitive to mis-alignment so don't throw the beam too far off axis. Retroreflection is usually the biggest headache in any coherent light optical train and care should be exercised to reduce it to a minimum.
A useful trick for reduction of retroreflection from an etalon such as this one is to put a small (≈1 mm) pinhole mask directly in front it and use only the very center of the beam. The pinhole restricts the allowed exit angles from the etalon in the direction towards the laser thus allowing a closer to on-axis alignment of the optics. The down side to this is the loss of input light but in our case, with over 5 mW, this wouldn't be a problem.
Just for kicks you may want to try full retroreflection back into the laser just to see how much trouble it can cause...
Make sure that the beam is centered on the face of the diode and the reflection is not going straight back into the laser output mirror but is slightly off center instead.
Set to 10k Ohm is a good tradeoff between gain and bandwidth. Try switching it to different values and observe the etalon/photodiode signal rolloff as a function of sawtooth frequency.
Trigger the 'scope with the sawtooth on channel A and observe the photodiode output on channel B. It may help to invert channel B because then the peaks correspond to the light on the photodiode (etalon in resonance condition).
I used DC coupling for both channels because I like to see exactly what I'm doing (or as close to it as the instrumentation will allow). I want to know about any offsets, if they exist, at the earliest time. In any event the sawtooth will become distorted on AC coupling.
Choose an appropriate time base. I used 1 ms per division because my sweep sawtooth was at 100 Hz.
We can choose between the rising or falling sections of the sawtooth -- the pattern of peaks on one slope will be a mirror image of the pattern on the other slope. How do we know which direction is low frequency and which is high frequency on the spectrum trace (channel B)? The easy and foolproof way to determine this is to cycle the power to the laser and observe the result.
Shut off the laser for about 30 seconds so that it cools down a little. When we turn the power back on we know that the laser tube is now expanding and the mirrors are getting further apart. When the mirrors are receding from the light in the cavity the light will be doppler shifted down in frequency and so we now know that the direction in which the peaks are moving is the low frequency direction. Now we can choose our trace with confidence without knowing what is going on in the Offset/Gain Stage or polarity of the oscilloscope inputs.
I our case the negative slope of the sawtooth corresponds to a sweep from low to high frequency as a function of the horizontal (x) axis of the 'scope.
The radius of curvature of the etalon mirrors is stated to be 2.50 cm in the instructions for the lab. The focal length of a spherical mirror is half its radius of curvature. Light rays from a point at inifnity will be turned through twice the angle that they make with the surface at the intersection point which means that in the small angle limit the point of intersection with the optical axis will be midway from the center of curvature and the point where the mirror intersects the optical axis. The etalon mirror spacing is the same as the radius of curvature of 2.50 cm. The round trip distance is 4 times the cavity length. Thus the round trip length is L = 10.0 cm.
The Free Spectral Range (FSR) of the interferometer is
FSR = c/L = (3.00·108 m/s)/(0.100 m) = 2.99 GHz ≈ 3.0 GHz
On the oscilloscope the FSR is the distance between repetitions of the peak structure. Today I measure an etalon mode spacing of x = 1.85±0.05 cm on the 'scope corresponding to a frequency of
f(x) = FSR/x = (3.0 GHz)/(1.85±0.05 cm) = 1620±150 MHz/cm
My measured laser cavity mode spacing seems to be (using the x10 scale):
Df = f(x) · (0.26±0.05 cm) = 420±90 MHz
Which leads to a coherence length of
Lc = c/Dn = c/(2·p·Df) = (3.00·108 m/s)/(2·p·(420±90 MHz))
≈ 12±3 cm
This is a valid measure of the coherence length provided the laser is not undergoing thermal cycling causing the modes to drift around under the gain curve too rapidly.
The use of only one laser cavity mode spacing rather than two is justified on the basis that when the modes are equal there are only two of them and when there are three of them the two non-central modes each have about half the power of the central one and so can only contribute half as much of an effect. Also the actual width of the modes is very much smaller than indicated by the peaks on the oscilloscope. The peaks appear wide because the etalon is not of a particularly high cavity finesse. An indication of how wide the peaks really are can be found by zooming in very close on one and observing the amount of frequency jitter (primarily from retroreflection) and noting that in order for this jitter to happen the laser cavity must be able to resolve it in frequency space. This can only happen if the line width of the laser is narrower than the frequency disturbance. Thus the limiting factor here is instability brought on by retroreflection.
If one could somehow exclude the adjacent laser cavity modes from the output beam one could achieve a much greater degree of stability. This could, in principle, be done with the use of a polarizer because the adjacent modes are orthogonally polarized due to mode competition. The only catch here is that the modes exchange polarization randomly because of the disturbance from retroreflection.
Just for kicks one could measure the real frequency stability of a single mode by noting the amount of frequency jitter of a single peak and using that instead of the mode spacing in th above calculation.
Coherence length in hand let us now get on with the business of doing an holography experiment.
Page first created Monday, March 27, 2000
Page last modified Wednesday, May 23, 2001 4:17 PM